AdaBoost
Boosting jest to rodzina algorytmów powszechnie wykorzystywanych w ramach uczenia maszynowego (ang. machine learning). W odróżnieniu od np. modelu regresji logistycznej czy drzew decyzyjnych boosting sam w sobie nie stanowi modelu w klasycznym rozumieniu tego słowa. Boosting jest przykładem rodziny tzw. ensemble method. Najogólniej rzecz ujmując, są to metody łączenia wielu modeli uczenia maszynowego w jeden finalny model. Innym przykładem rodziny tego typu jest np. Bagging, do której zalicza się m.in. Random Forest. Z kolei najpopularniejszym przedstawicielem algorytmu z rodziny boosting jest XGBoost - Extreme Gradient Boosting. XGBoost zawdzięcza dużą popularność przede wszystkim swojej wysokiej skuteczności, wygrywając niejednokrotnie nawet z głębokimi sieciami neuronowymi (ang. deep learning), zwłaszcza w przypadku danych tabelarycznych1.
Boosting jako metoda ensemble łączy wiele tzw. modeli bazowych w jeden model predykcyjny. Wyróżniającymi cechami algorytmów z tej rodziny jest wykorzystanie tzw. słabych klasyfikatorów (ang. weak learners) oraz modyfikacja zbioru uczącego w trakcie uczeniu kolejnych modeli. Przez słabe klasyfikatory należy rozumieć modele, których skuteczność jest jedynie niewiele lepsza od losowych predykcji (np. rzut monetą). W odróżnieniu od nich tzw. silnie klasyfikatory cechują się już odpowiednio wysoką skutecznością.
Jednym z klasycznych algorytmów typu boosting jest AdaBoost, który został opracowany przez Freund oraz Schapire w 1997 roku2. Poznanie tego algorytmu stanowi dobry wstęp przed zagłębieniem się w bardziej skomplikowane algorytmy z tej rodziny. W tekście opisujemy działanie AdaBoost oraz przedstawiamy prostą implementację w Python.
AdaBoost
AdaBoost jest algorytmem typu boosting, którego wyróżniają następujące elementy:
1) Sekwencyjne uczenie słabych klasyfikatorów
Działanie algorytmu możemy podzielić na iteracje. W każdej iteracji uczony jest pojedynczy klasyfikator. Z reguły modelem bazowym wykorzystywanym przez AdaBoost jest drzewo decyzyjne z pojedynczym wierzchołkiem oraz dwoma liśćmi. Jest to możliwie najprostsze drzewo decyzyjne, które określane jest mianem stump.
Dodatkowo każdemu klasyfikatorowi przypisywana jest waga, której wartość zależy od jego skuteczności na próbie uczącej. Wagi te wykorzystywane są w późniejszym etapie do wygenerowania finalnej predykcji.
2) Modyfikacja próby uczącej za pośrednictwem wag nazwanych obserwacją
AdaBoost modyfikuje pośrednio zbiór uczący poprzez nadanie wag poszczególnym obserwacją. Nie należy mylić tych wag, z wagami przypisywanymi poszczególnym modelom, o których pisaliśmy w poprzednim paragrafie. Wagi odgrywają bardzo istotną rolę w trakcje uczenia klasyfikatorów. Określają one, w jakim stopniu dana obserwacja ma wpływ na wartość funkcji celu, która podawana jest optymalizacji. Obserwacje z większymi wagami są bardziej istotne i mają większy wpływ na parametry obecnie uczonego modelu.
Podczas uczenia pierwszego modelu, wagi wszystkich obserwacji mają identyczną wartość. W kolejnych iteracjach są one aktualizowane na podstawie predykcji poprzednich klasyfikatorów. Wagi obserwacji, które zostały błędnie sklasyfikowane, są odpowiednio zwiększane. Powoduje to, że w trakcie uczenia kolejnych modeli, obserwacji te będą miały większe znaczenie. Sytuacja wygląda odwrotnie w przypadku obserwacji, które zostały poprawnie sklasyfikowane. Ich wagi zostaną odpowiednio zmniejszone. Tym samym kolejne klasyfikatory będą musiały się bardziej skupić na tych trudniejszych do zaklasyfikowania obserwacjach.
3) Generowanie finalnej predykcji poprzez wykorzystanie ważonego głosowania
W metodach opartych o łączenie wielu modeli do ustalenia finalnej predykcji wykorzystywany jest z reguły mechanizm głosowania. Modele bazowe na podstawie swoich predykcji głosują na poszczególne klasy (np. spam, nie spam). Następnie jako finalną predykcję ustala się klasę, która otrzymała najwięcej głosów. Podobny mechanizm wykorzystywany jest przez AdaBoost. Jedyna modyfikacja polega na ważeniu głosów poszczególnych klasyfikatorów. Głosy ważone są za pomocą wag przypisanym klasyfikatorom, o których wspominaliśmy powyżej. Modele z większymi wagami będą miały większy wpływ na finalną predykcję.
Algorytm AdaBoost nie jest skomplikowany. Korzystając z pseudokodu możemy zapisać go w kilku krokach.
- Zainicuj początkowe wagi obserwacji
- Powtórz \(N\) razy:
- Wytrenuj klasyfikatora
- Oblicz błąd klasyfikatora
- Oblicz wagę klasyfikatora
- Zaktualizuj wagi obserwacji
- Zapisz klasyfikator oraz jego wagę
- Wygeneruj finalną predykcję wykorzystując ważone głosowanie
Bardziej szczegółowy opis powyższych kroków znajduje się w kolejnej części tekstu.
AdaBoost - Zapis Matematyczny
Niech \(\{ ({\bf x_i }, y_i) \}_{i=1}^{N}\) będzie zbiorem uczącym zawierającym \(N\) obserwacji. Każda obserwacja \(({\bf x }, y)\) złożona jest z wektora zmiennych \({\bf x }\) oraz zmiennej celu \(y\), która przyjmuje wartości ze zbioru \(\{-1, 1\}\). Wynikiem działania algorytmu jest \(M\) słabych klasyfikatorów \(G_m(x)\), których predykcje łączone są poprzez ważone głosowanie zgodnie z poniższą formułą:
\(G(x) = sign \left( \sum_{i=1}^{M} \alpha_m G_m(x) \right)\),
gidze \(\alpha_m\) to waga \(m\)-tego klasyfikatora.
- Inicializacja wag wszystkich obserwacji identyczną wartością \(w_i = 1/N, i = 1, 2, . . . , N\)
- Pętla \(m = 1\ ...\ M\):
- Uczenie klasyfikatora \(G_m(x)\) na próbie uczącej ważonej wagami \(w_i\).
-
Obliczenie błędu klasfyikatora:
\(err_m = \sum_{i=1}^{N} w_i I(y_i \neq G_m(x)_i)\) \(I(y_i \neq G_m(x_i)) = \begin{cases} 1 & y_i \ne G_m(x_i) \\ 0 & y_i = G_m(x_i) \end{cases}\)
-
Obliczenie wagi klasyfikatora
\[\alpha_m = \frac{1}{2} \log \frac{1 - err_m}{err_m}\] -
Akutalizacja wartości wag obserwacji
\[w_i = w_ie^{-\alpha_m y_i G_m(x_i)}, i = 1, 2, ..., N\] -
Normalizacja wag obserwacji
\[w_i = \frac{w_i}{\sum_{i=1}^{N} w_i}, i = 1, 2, ..., N\]
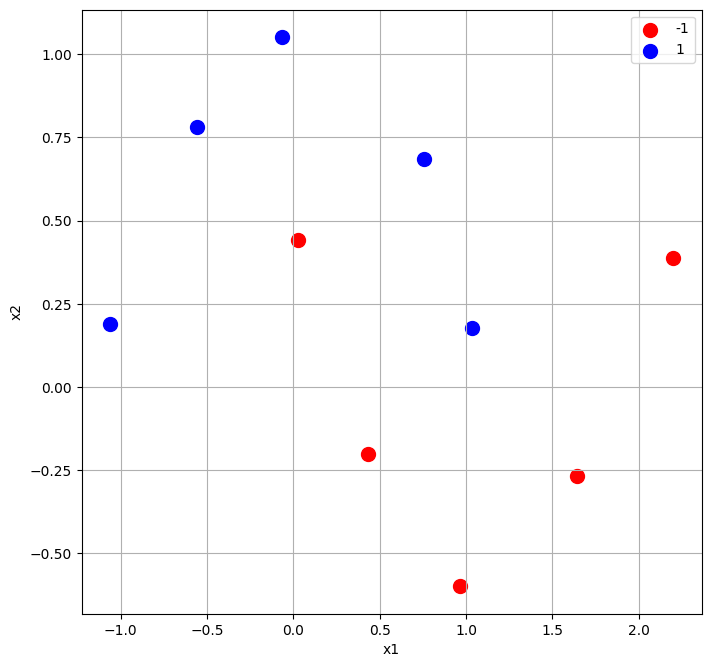
W dalszej części tekstu omówimi dokładnie poszczególne kroki algorytmu. Dla zobrazowania pojedynczej iteracji wykorzystamy losowo wygenerowany zbiór danych złożony z 10 obserwacji. Zawiera on dwie zmienne objaśniające: x1 i x2 oraz zmienną celu y. Tabela 1 zawiera wartości wszystkich zmiennych. Z kolei na rysunku 1 przedstawiono obserwacje w podziale na klasy (1 - niebieski, -1 - czerwony).
| x1 | x2 | y | |
|---|---|---|---|
| 0 | 1.6407 | -0.2677 | -1 |
| 1 | -0.0651 | 1.0513 | 1 |
| 2 | 0.0262 | 0.4417 | -1 |
| 3 | 0.4297 | -0.2018 | -1 |
| 4 | -0.5580 | 0.7827 | 1 |
| 5 | 0.7541 | 0.6837 | 1 |
| 6 | 1.0354 | 0.1784 | 1 |
| 7 | 0.9650 | -0.5990 | -1 |
| 8 | -1.0634 | 0.1899 | 1 |
| 9 | 2.1997 | 0.3881 | -1 |
Algorytm
1. Inicializacja wag wszystkich obserwacji identyczną wartością \(w_i = 1/N, i = 1, 2, . . . , N\)
Nasz przykładowy zbiór zawiera 10 obserwacji, stad przypisujemy każdej z nich identyczną wagę równą \(1/10 = 0.1\).
| x1 | x2 | y | w | |
|---|---|---|---|---|
| 0 | 1.6407 | -0.2677 | -1 | 0.1 |
| 1 | -0.0651 | 1.0513 | 1 | 0.1 |
| 2 | 0.0262 | 0.4417 | -1 | 0.1 |
| 3 | 0.4297 | -0.2018 | -1 | 0.1 |
| 4 | -0.5580 | 0.7827 | 1 | 0.1 |
| 5 | 0.7541 | 0.6837 | 1 | 0.1 |
| 6 | 1.0354 | 0.1784 | 1 | 0.1 |
| 7 | 0.9650 | -0.5990 | -1 | 0.1 |
| 8 | -1.0634 | 0.1899 | 1 | 0.1 |
| 9 | 2.1997 | 0.3881 | -1 | 0.1 |
2. Pętla \(m = 1\ ...\ M\):
Liczba iteracji \(M\) jest hiperperparametrem, który w najlepszym przypadku należy poddać optymalizacji. Ewentualnie można przedwcześnie zakończyć działanie algorytmu w wyniku zaobserwowania pogarszania się skuteczności modelu na próbie walidacyjnej.
2.1. Uczenie klasyfikatora \(G_m(x)\) na próbie uczącej ważonej wagami \(w_i\).
Na rysunku 2 przedstawio drzewo decyzyjne z pojedynczym wierzchołkiem nauczone na naszym przykładowym zbiorze. Analizując to drzewo, możemy dojść do wniosku, że jest to naprawdę bardzo prosta reguła decyzyjna. W przypadku spełnienia warunku \(x_1 \leq -0.019\) obserwacja zostanie zaklasyfikowana jako \(-1\). W przeciwnym razie trafi do drugiej klasy \(1\).

2.2. Obliczenie błędu klasfyikatora:
\(err_m = \sum_{i=1}^{N} w_i I(y_i \neq G_m(x)_i)\) \(I(y_i \neq G_m(x_i)) = \begin{cases} 1 & y_i \ne G_m(x_i) \\ 0 & y_i = G_m(x_i) \end{cases}\)
Krok ten sprowadza się do sumowania wag dla niepoprawnie sklasyfikowanych obserwacji. Dla naszego zbioru, zostały one oznaczone na rysunku 3. Dodatkowo przedstawiono granicę decyzyjną wynikająco z drzewa decyzyjnego.
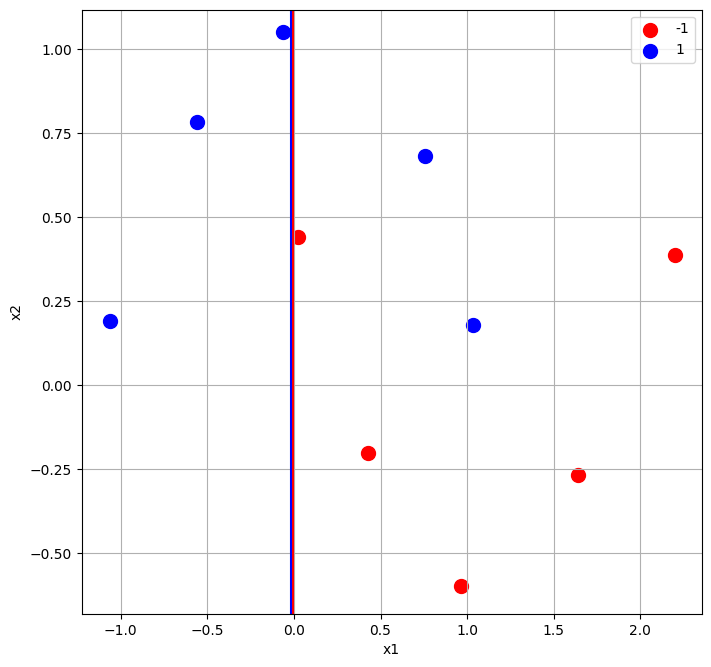
Dwie obserwacje zostały niepoprawnie sklasyfikowane jako \(-1\) (czerwone). Są to obserwacje o indeksach 5 oraz 6 (patrz Tabela 3). Predykcja wynikająco z modelu \(pred\) różni się dla nich od wartośći zmiennej celu \(y\).
| x1 | x2 | y | w | pred | |
|---|---|---|---|---|---|
| 0 | 1.6407 | -0.2677 | -1 | 0.1 | -1 |
| 1 | -0.0651 | 1.0513 | 1 | 0.1 | 1 |
| 2 | 0.0262 | 0.4417 | -1 | 0.1 | -1 |
| 3 | 0.4297 | -0.2018 | -1 | 0.1 | -1 |
| 4 | -0.5580 | 0.7827 | 1 | 0.1 | 1 |
| 5 | 0.7541 | 0.6837 | 1 | 0.1 | -1 |
| 6 | 1.0354 | 0.1784 | 1 | 0.1 | -1 |
| 7 | 0.9650 | -0.5990 | -1 | 0.1 | -1 |
| 8 | -1.0634 | 0.1899 | 1 | 0.1 | 1 |
| 9 | 2.1997 | 0.3881 | -1 | 0.1 | -1 |
Aby policzyć błąd klasyfikatora musimy jedynie sumowac wagi tych dwóch obserwacji. Jest to tożsame z liczeniem średniego ważonego błędu klasyfikatora. W tym wypadku, formuła jest bardzo prosta, ponieważ wagi wszystkich obserwacji sumują się do jedności, stąd w mianowniku przy liczeniu średniej otrzymalibyśmy jeden.
\[err_1 = 0.1 + 0.1 = 0.2\]2.3. Obliczenie wagi klasyfikatora
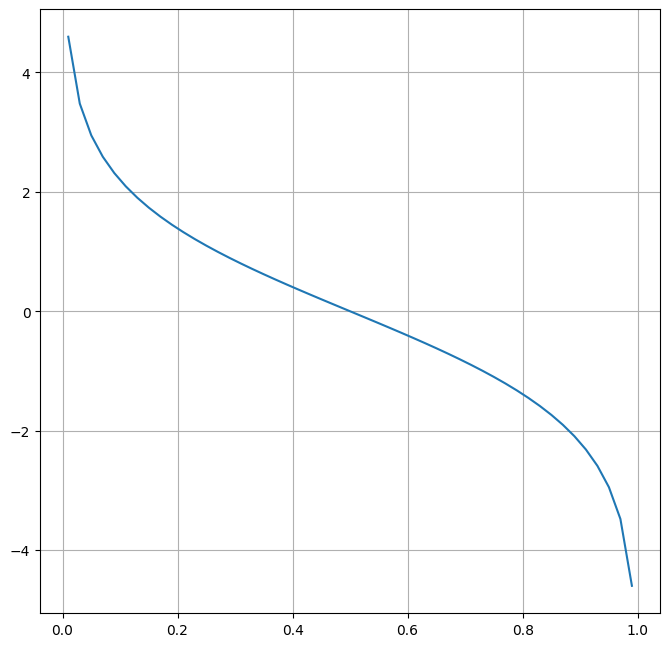
\[\alpha_m = \frac{1}{2} \log \frac{1 - err_m}{err_m}\]Waga klasyfikatora, jak już wcześniej wspomniano, zależy od jego błędu na próbie uczącej. Rysunek 4 zawiera wykres formuły liczącej wagę klasyfikatora. Na osi poziomej zaznaczono poziom błądu, który przyjmuje wartości z przedziału \(<0; 1>\). Możemy zauważyć, że czym niższy błąd, tym waga klasyfikatora będzie większa. W przypadku błędu klasyfikacji równego 0.5, co jest tożsame z losową predykcją, waga klasyfikatora zostanie ustalona na zero. Oznacza to, że predykcje modelu zostaną całkowicie pominięte w póżniejszym głosowaniu. Z kolei jeżeli błąd klasyfikatora jest większy od 0.5, waga klasyfikatora będzie ujemna. W takiej sytuacji, predykcje modelu będą niejako traktowane odwrotnie.
W naszym obecnym przykładzie, błąd klasyfikatora wyniósł 0.2. Stąd waga klasyfikatora wyniesie:
\[\alpha_1 = \frac{1}{2} \log \frac{1 - 0.2}{0.2} = \frac{1}{2} \log 4 = 0.69315\]2.4. Akutalizacja wartości wag obserwacji
\[w_i = w_ie^{-\alpha_m y_i G_m(x_i)}, i = 1, 2, ..., N\]Ponieważ założyliśmy, że \(y_i \in \{-1, 1\}\) oraz \(G_m(x_i) \in \{-1, 1\}\), to wynika z tego, że iloczyn \(y_i G_m(x_i)\) może przyjąć tylko dwie wartości: \(-1\) oraz \(1\). Jeżeli \(y_i = G_m(x_i)\), to ich iloczyn wyniesie \(1\). W przeciwnym przypadku, kiedy obserwacji zostanie błędnie sklasyfikowania, wyniesie on \(-1\). Tym samym możemy inaczej sformułować formułę akutalizujacą wagi:
\[w_i = \begin{cases} w_i e^{\alpha_m} & y_i \ne G_m(x_i) \\ w_i e^{-\alpha_m} & y_i = G_m(x_i) \end{cases}\]Waga klasyfikatora \(\alpha_m\) może być ujemna lub dodatnia (pomijamy sytuacje kiedy jest zerowa). W zależności od tego oraz wyniku predykcji (błedna, poprawna) dla danej obserwacji, możemy wyróżnić cztery sytuacje, jeżeli chodzi o zmianę wagi tej obserwacji:
| Predykcja | \(\alpha_m > 0\) | \(\alpha_m < 0\) |
|---|---|---|
| Błędna \(y_i \ne G_m(x_i)\) | Podnieś | Obniż |
| Poprawna \(y_i = G_m(x_i)\) | Obniż | Podnieś |
Wynika z tego, że wagi obserwacji, które zostały błędnie sklasyfikowane przez klasyfikator z dodatnią wagą, zostaną zwiększone. Z kolei wagi obserwacji, które zostały poprawnie sklasyfikowane przez ten sam klasyfikator, zostaną obniżone.
W naszym przykładzie, wagi poprawnie oraz błędnie sklasyfikowanych obserwacji zostaną odpowiednio obniżone do 0.05 oraz podwyższone do 0.20.
| x1 | x2 | y | w | pred | |
|---|---|---|---|---|---|
| 0 | 1.6407 | -0.2677 | -1 | 0.05 | -1 |
| 1 | -0.0651 | 1.0513 | 1 | 0.05 | 1 |
| 2 | 0.0262 | 0.4417 | -1 | 0.05 | -1 |
| 3 | 0.4297 | -0.2018 | -1 | 0.05 | -1 |
| 4 | -0.5580 | 0.7827 | 1 | 0.05 | 1 |
| 5 | 0.7541 | 0.6837 | 1 | 0.20 | -1 |
| 6 | 1.0354 | 0.1784 | 1 | 0.20 | -1 |
| 7 | 0.9650 | -0.5990 | -1 | 0.05 | -1 |
| 8 | -1.0634 | 0.1899 | 1 | 0.05 | 1 |
| 9 | 2.1997 | 0.3881 | -1 | 0.05 | -1 |
2.5. Normalizacja wag obserwacji
\[w_i = \frac{w_i}{\sum_{i=1}^{N} w_i}, i = 1, 2, ..., N\]W ostatnim kroku musimy jedynie znormalizować wagi zaktualizowane w poprzednim kroku, tak aby sumowały się do jedności. W tym celu każdą wagę obserwacji należy podzielić przez ich obecną sumę.
Dla naszego zbioru danych, po akutalizacji wagi sumują się do \(0.80\). Po normalizacji będa wyglądać następująco.
| x1 | x2 | y | w | pred | |
|---|---|---|---|---|---|
| 0 | 1.6407 | -0.2677 | -1 | 0.0625 | -1 |
| 1 | -0.0651 | 1.0513 | 1 | 0.0625 | 1 |
| 2 | 0.0262 | 0.4417 | -1 | 0.0625 | -1 |
| 3 | 0.4297 | -0.2018 | -1 | 0.0625 | -1 |
| 4 | -0.5580 | 0.7827 | 1 | 0.0625 | 1 |
| 5 | 0.7541 | 0.6837 | 1 | 0.2500 | -1 |
| 6 | 1.0354 | 0.1784 | 1 | 0.2500 | -1 |
| 7 | 0.9650 | -0.5990 | -1 | 0.0625 | -1 |
| 8 | -1.0634 | 0.1899 | 1 | 0.0625 | 1 |
| 9 | 2.1997 | 0.3881 | -1 | 0.0625 | -1 |
Ostatecznie wagi poprawnie sklasyfikowanych obserwacji zostaną obnizone do 0.0625. Natomiast wagi błędnie sklasyfikowanych obserwacji zostną podwyższone do 0.25. Podczas uczenia kolejnego modelu, obserwacje te będą miały niemal cztero-krotnie większe znaczenie.
AdaBoost - Implementacja w Python
Wszystkie kody i skrypty dostępne są w repozytorium GitHub.
Znając mechanizm funkcjonowania algorytmu AdaBoost, możemy przystąpić do jego implementacji. Stworzymy klasę AdaBoostClassyfier, która będzie posiadała podobny interfejs jak większość estymatorów z popularnego pakietu scikit-learn. Interfejs ten będzie udostępniał jedynie dwie metody: fit oraz predict. Pierwsza z nich odpowiadała będzie za uczenie modeli, druga za generowanie predykcji.
W pierwszej kolejności zdefiniujemy metodę inicjalizują, która będzie przyjmowała dwa parametry: base_classifier - model bazowy, zakładamy, że będzie to estymator z pakietu scikit-learn np. DecisionTreeClassifier, oraz n_classifiers - liczba klasyfikatorów. Dodatkowo inicjalizujemy zmienną wewnętrzna classifiers, która będzie przechowywała listę klasyfikatorów wraz z ich wagami.
1
2
3
4
def __init__(self, base_classifier, n_classifiers):
self.base_classifier = base_classifier
self.n_classifiers = n_classifiers
self.classifiers = []
W metodzie fit zaimplementujemy pętlę uczącą kolejne klasyfikatory. Przyjmuje ona dwa parametry: macierz ze zmiennymi X oraz wektor zmiennej celu y. W pierwszej kolejności inicjalizujemy wagi obserwacji. Następnie w pętli wywołujemy wewnętrzną metodę _fit_classifier, która odpowiada za uczenie pojedynczego klasyfikatora.
1
2
3
4
5
def fit(self, X, y):
'''Build a boosted classifier.'''
weights = np.full(X.shape[0], 1/X.shape[0])
for i in range(self.n_classifiers):
weights = self._fit_classifier(X, y, weights)
Metoda _fit_classifier realizuje wszystkie zadania w ramach pojedynczej iteracji algorytmu. Na początku musimy pamiętać o sklonowaniu obiektu reprezentującego bazowy model. W przeciwnym przypadku wszystkie klasyfikatory będą wskazywały na ten sam obiekt. Następnie uczymy klasyfikator oraz generujemy jego predykcje. W kolejnych krokach liczymy błąd klasyfikatora poprzez sumowanie wag błędnie sklasyfikowanych obserwacji oraz aktualizujemy wagi obserwacji. Zapisujemy też obecny model oraz jego wagę w zmiennej wewnętrznej classifiers.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def _fit_classifier(self, X, y, weights):
clf = sklearn.base.clone(self.base_classifier)
clf.fit(X, y, sample_weight=weights)
yhat = clf.predict(X)
error = weights[y != yhat].sum()
clf_weight = 0.5*np.log((1 - error)/error)
weights = weights*np.exp(-yhat*y*clf_weight)
weights = weights/weights.sum()
self.classifiers.append((clf, clf_weight))
return weights
Metoda predict odpowiada za generowanie predykcji. W pierwszym kroku wywołujemy analogiczną metodę dla wszystkich bazowych modeli, aby uzyskać ich predykcje, które dodatkowo mnożymy przez wagę danego klasyfikatora. Następnie sumujemy wszystkie predykcje na poziomie obserwacji. Z tego względu, że zmienna celu przyjmuje wartości ze zbioru \(\{-1, 1\}\), na podstawie samego znaku wcześniej już wspomnianej sumy jesteśmy w stanie określić finalną predykcję.
1
2
3
4
5
6
7
8
def predict(self, X):
'''Predict classes.'''
preds = [
clf_weight*clf.predict(X)
for clf, clf_weight in self.classifiers
]
preds = np.stack(preds, axis=1)
return np.array([1 if x > 0 else -1 for x in preds.sum(axis=1)])
Cała klasa AdaBoostClassyfier prezentuje się następująco.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class AdaBoostClassifier:
'''An AdaBoost classifier.'''
def __init__(self, base_classifier, n_classifiers):
self.base_classifier = base_classifier
self.n_classifiers = n_classifiers
self.classifiers = []
def fit(self, X, y):
'''Build a boosted classifier.'''
weights = np.full(X.shape[0], 1/X.shape[0])
for i in range(self.n_classifiers):
weights = self._fit_classifier(X, y, weights)
def _fit_classifier(self, X, y, weights):
clf = sklearn.base.clone(self.base_classifier)
clf.fit(X, y, sample_weight=weights)
yhat = clf.predict(X)
error = weights[y != yhat].sum()
clf_weight = 0.5*np.log((1 - error)/error)
weights = weights*np.exp(-yhat*y*clf_weight)
weights = weights/weights.sum()
self.classifiers.append((clf, clf_weight))
return weights
def predict(self, X):
'''Predict classes.'''
preds = [
clf_weight*clf.predict(X)
for clf, clf_weight in self.classifiers
]
preds = np.stack(preds, axis=1)
return np.array([1 if x > 0 else -1 for x in preds.sum(axis=1)])
W pakiecie scikit-learn dostępny jest analogiczny klasyfikator sklearn.ensemble.AdaBoostClassifier.
AdaBoost - Implementacja w Python - Przykład Użycia
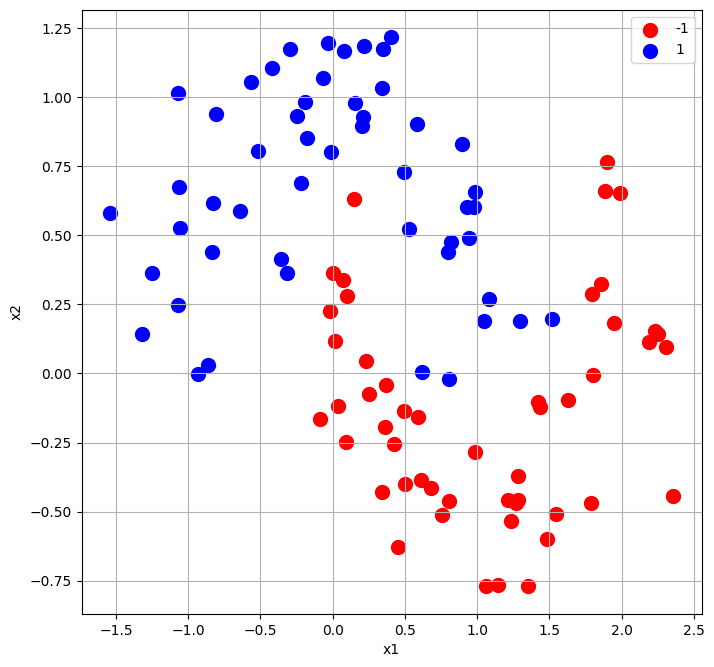
Na zakończenie wykorzystamy naszą implementację algorytmu AdaBoost dla przykładowego losowego zbioru danych, który został zobrazowany na rysunku 5.
Kod wywołujący AdaBoostClassifier jest bardzo prosty.
1
2
3
4
ada = AdaBoostClassifier(DecisionTreeClassifier(max_depth=1), 50)
ada.fit(X, y])
preds = ada.predict(X)
Na rysunku 6 przedstawiono granicę decyzyjną wynikająco z zastosowania AdaBoost.
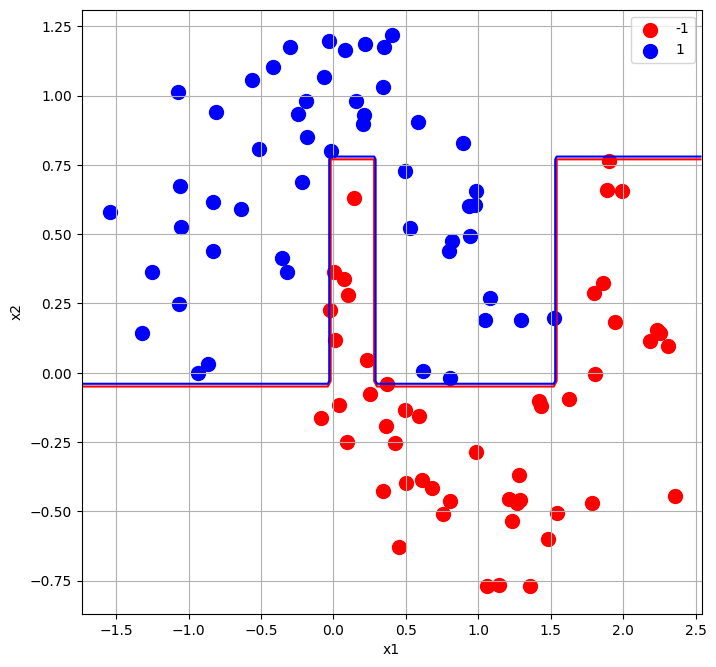
Podsumowanie
W tekście opisaliśmy jeden z klasycznych algorytmów typu boosting - AdaBoost. Skupiliśmy się jedynie na wykorzystaniu go dla celów klasyfikacyjnych. Istnieje jednak możliwość rozszerzenia samego algorytmu do zadań regresyjnych. Dla lepsze zrozumienia działania algorytmu przedstawiliśmy również własną implementację. Wykorzystując AdaBoost w praktyce, należy jednak skorzystać z gotowych i sprawdzonych rozwiązań, jak np. sckit-learn. Obecnie AdaBoost nie jest już za bardzo wykorzystywany. Został wyparty przez skuteczniejsze metody jak np. gradient boosting. Pomimo wszystko, warto znać ten algorytm, jako że stanowi punkt wyjścia do bardziej skomplikowanych metod.
-
Ravid Shwartz-Ziv, Amitai Armon, Tabular Data: Deep Learning is Not All You Need, 2021 Jun 6. ↩
-
Yoav Freund, Robert ESchapire, A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting, Journal of Computer and System Sciences Volume 55, Issue 1, August 1997, Pages 119-139 ↩